How to Develop Problem-Solving Skills for JEE Effectively

During my JEE preparation, I identified several important strategies to enhance my ability to solve tough problems and truly understand how to develop problem-solving skills for JEE. Many of these approaches were highlighted by my teachers at VMC. In this blog, I share a structured list of such methods to help students solve problems more efficiently and prepare effectively for JEE Advanced 2026. Towards the end, we also solve a seemingly difficult JEE Advanced 2025 Physics problem by applying these tactics.

How to develop problem-solving skills for JEE?

Ask yourself if this problem reminds you of some other problem or idea

If you have seen something similar before, you are more likely to solve the problem. While this observation is simple, you might still need to improvise a little to solve the problem.
If the problem even weakly resembles one you have solved before, it is worthwhile to make this problem look like the one you have already solved. For example, in Mathematics, this may involve adding and subtracting a few terms, substituting, etc. so that it is reduced to something of the form you already know.
Pay attention to the details in the question; it is possible that you recognise why the problem is framed like it is. It might be the given data or even the options that can sometimes inspire a solution.
If you come across a novel technique, understand it and then memorise it. For example, one technique I came across during my JEE Preparation was that “If you can’t solve equality, set up a system of inequalities.”

Simplify the Problem

The first step in solving a hard problem is to simplify it as much as possible. For example, in Mathematics this might mean squaring to get rid of the square root or dividing the problem into sub-problems.
Also, we try to recognise an intermediate C such that A naturally leads to C and then C leads to B, hence establishing the required connection between A and B.
It might also be some elementary checks. For instance, Dimensional Analysis in a Physics problem. Also, break down the problem, test smaller cases, or weaker conditions first. In Mathematics, a difficult combinatorics problem is often approached by considering a smaller test case first.

Exhaustive Search

In some cases, it is best to list down or mentally keep track of all the tools and techniques related to the problem. Then eliminate one at a time. Eventually, this often leads to a solution or inspiration to look elsewhere.
For example, in an Ionic Equilibrium problem, you shall first identify the case, such as Acid-Base, Salt Hydrolysis, Buffer Solution, etc. Then clearly write all the equilibrium reactions involved. Now, think about all the approximations you have seen and can be applied in the given case. Then judge which one is most logical. Thus, in Ionic Equilibrium, one should memorise the formulas but also the limited number of approximation patterns that are applied to arrive at all these formulas.
In Mechanics problems, identify the unknowns and think about writing all the equations describing the system. Then think about conserving momentum/angular momentum, try different frames of reference to apply these conservations, work-energy, etc. Therefore, by exhaustively applying your tools, you can write all the equations.
With practice, this search becomes a rapid mental checklist that often takes only a few seconds.

Also Read: Why Students Score Highest in Chemistry

Restate the Problem

Look at the problem in different ways. In Mathematics, this might mean rephrasing an algebraic problem geometrically. This is particularly useful in Linear Algebra. In Physics, some problems are easily solved by describing the problem using vectors. Let us demonstrate this idea on a JEE Advanced 2025 Physics Problem.

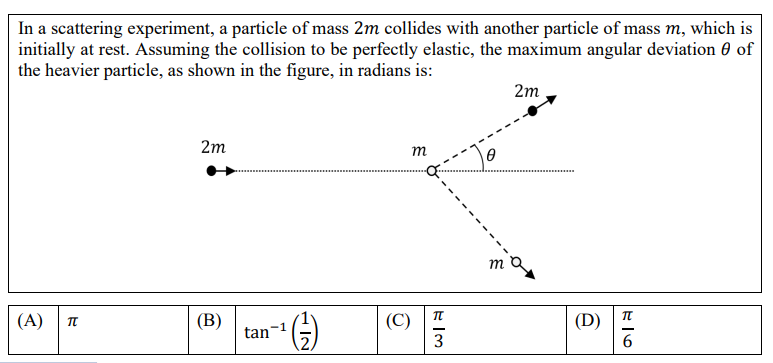
If you have familiarity with such a system of particles, you would be able to think of possible ways to solve this problem. Initially, solving this problem in the ground frame appears complicated. There are multiple unknown variables after the collision, but you need to focus on maximising the deviation. Thus, the ground frame approach appears calculative.

Step 1: Exhaustive Search

Conservation of Linear Momentum
Conservation of Kinetic Energy (Elastic Collision)
Choice of Reference Frame (Ground or Centre of Mass Frame)
Vector Representation of Velocities and Conservation of Momentum

Step 2: Simplification and Restating

In the absence of external force, the COM frame is inertial. Shifting to the COM frame is a natural choice and is also a familiar idea.
Moreover, using vectors to maximise angle or magnitude under given constraints is quite common in such problems. So, we can restate the problem geometrically.
Here, we identify the constraints as momentum conservation and kinetic energy conservation.

Solution:

Let the initial velocity vector of 2m be v.
Final velocity of COM = Initial velocity of COM = v_CM
In COM frame, final velocity of 2m with respect to COM is v₁^CMand similarly for m is v₂^CM
By conservation of energy, one can show that the initial speed of either mass remains the same before and after collision.
Thus, we can represent this situation as follows using a vector diagram for v_CM + v₁^CM= v₁(Final Velocity of 2m in ground frame).

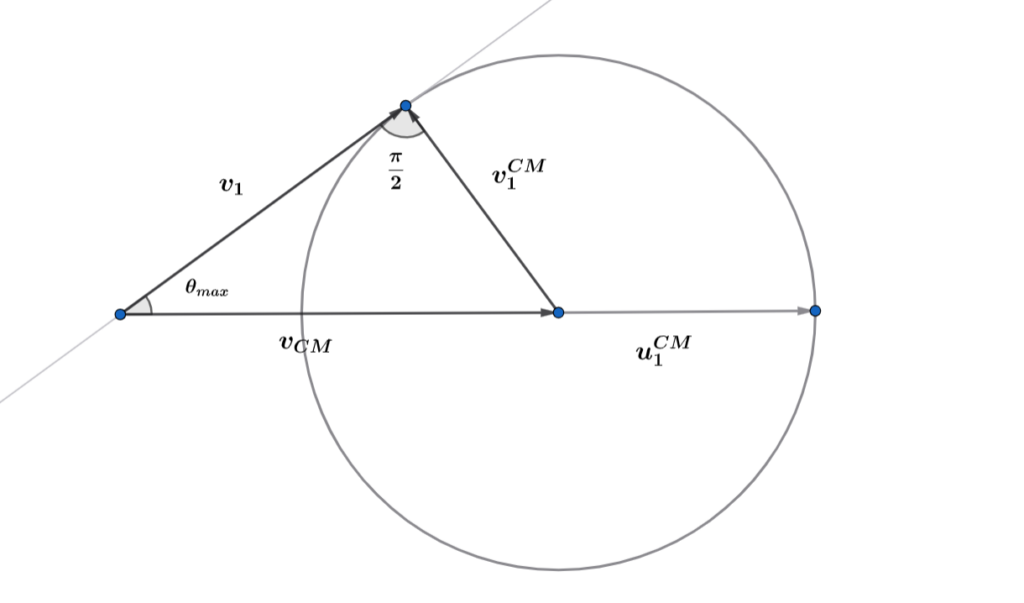
Figure: Vector construction in the centre-of-mass frame illustrating that the maximum angular deviation occurs when v₁^CMis perpendicular to v_CM.

From the geometry of the construction, we obtain sin(θₘₐₓ) = |v₁^CM|/|v_CM| = 1/2, hence θₘₐₓ = π/6.

Conclusion

Difficult problems are rarely solved by a single brilliant idea. More often, they yield when familiar patterns are recognised, unnecessary complexity is removed, and the problem is restated in a form that exposes its structure.

What appears as an insight in a final solution is usually the result of systematic thinking developed through practice. By consciously building these habits, problem-solving becomes faster and more reliable, especially under exam conditions.

Frequently Asked Questions (FAQs)

Do these strategies slow down problem-solving during exams?

No. While the reasoning process is presented in detail in the examples, with enough practice, these checks occur quickly and often unconsciously. When working under a time constraint, such as in an exam, identifying structure and eliminating unproductive approaches early typically improves speed.

Are these techniques meant only for very difficult problems?

No. These techniques are useful in problems of all levels of difficulty. In simpler ones they act almost automatically, while in more difficult ones they prevent one from getting stuck or engaging in excessively long calculations.

How long does it take to develop these habits of thinking?

These habits develop gradually through regular practice. Initially, the process may feel deliberate, but over time it becomes faster and more intuitive as familiarity with problem structures increases.

Does this method work across all subjects in JEE?

Yes. The principles – recognition, simplification, systematic investigation, and restatement apply equally to Mathematics, Physics and Chemistry, even though their specific applications may differ.

Should I practice these strategies separately from solving problems?

No separate practice is required. These strategies are best developed alongside regular problem-solving by reflecting on why a particular approach worked after solving a problem.